7 способов найти площадь прямоугольника
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7.
 Если известны радиус описанной окружности и угол между диагоналями
Если известны радиус описанной окружности и угол между диагоналямиНайдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
Площадь прямоугольника — формул, пример расчет, калькулятор
Прямоугольник – это параллелограмм, у которого все углы равны 90°, а противоположные стороны попарно параллельны и равны.
У прямоугольника есть несколько неопровержимых свойств, которые применяются в решении множества задач, в формулах площади прямоугольника и его периметра. Вот они:
- Стороны прямоугольника являются его высотами;
- Длины диагоналей равны между собой ;
- Точка пересечения диагоналей делит их пополам;
Длина неизвестной стороны или диагонали прямоугольника вычисляется по формуле площади прямоугольного треугольника или по теореме Пифагора. Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:
Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:
Пример расчета площади прямоугольника по этой формуле очень прост. Зная две стороны, к примеру a =3 см, b = 5 см, мы легко высчитаем площадь прямоугольника:
Площадь прямоугольника через диагонали
Иногда требуется применить формулу площади прямоугольника через диагонали. Для нее потребуется не только узнать длину диагоналей, но и угол между ними:
Рассмотрим пример расчета площади прямоугольника через диагонали. Пусть дан прямоугольник с диагональю d = 6 см и углом = 30°. Подставляем данные в уже известную формулу:Итак, пример расчета площади прямоугольника через диагональ показал нам, что найти площадь таким образом, если задан угол, довольно просто.
Рассмотрим еще одну интересную задачку, которая поможет нам немного размять мозги.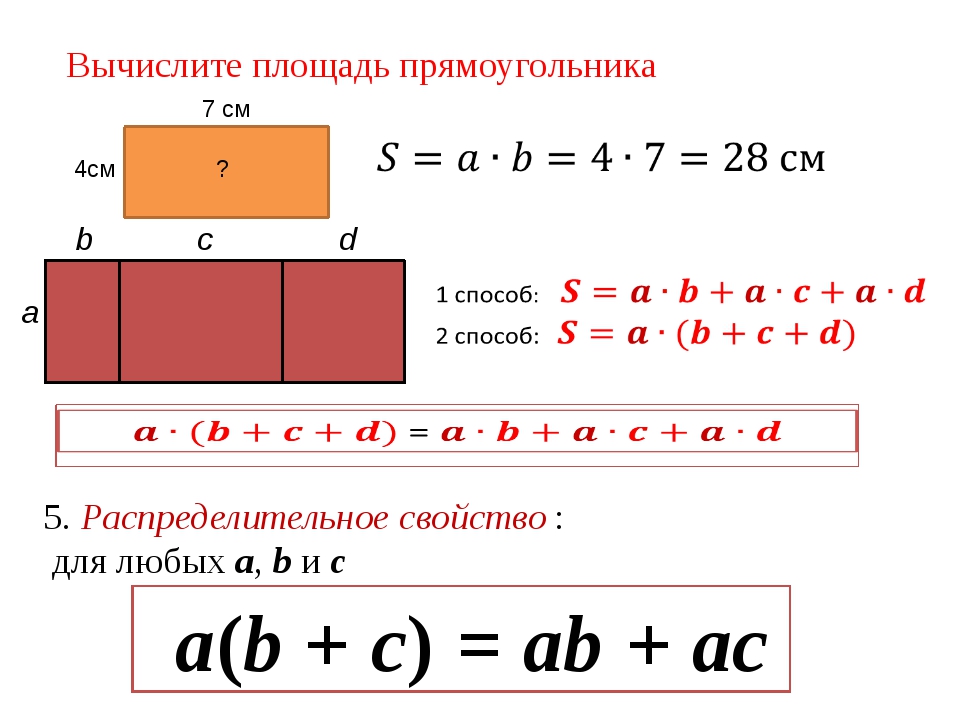
Итак, у нас есть несколько условий. Для наглядности запишем их, чтобы увидеть все известные и неизвестные параметры:
Стороны фигуры попарно параллельны и равны. Поэтому периметр фигуры равен удвоенной сумме длин сторон:
Из формулы площади прямоугольника, которая равняется произведению двух сторон фигуры, найдем длину стороны b
Отсюда:
Подставляем известные данные и находим длину стороны b:
Рассчитываем периметр фигуры:
Вот так, зная несколько легких формул, можно вычислить периметр прямоугольника, зная его площадь.
Площади фигур — Сайт учителя математики
Друзья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
S трапеции ты знаешь.

Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.
С понятием площади нам приходиться сталкиваться ежедневно. Для того, чтобы постелить новую плитку в вашей квартире вам нужно приобрести определенное ее количество, которое будет зависеть от площади вашей комнаты. Размер земельного участка вашего дома также будет характеризоваться площадью. Обычно люди забывают как найти площадь более сложных фигур, таких как треугольник, трапеция, или круг, но если вы настолько закрутились в жизни, что забыли как найти площадь прямоугольника, то мы вам это напомним в данной статье.
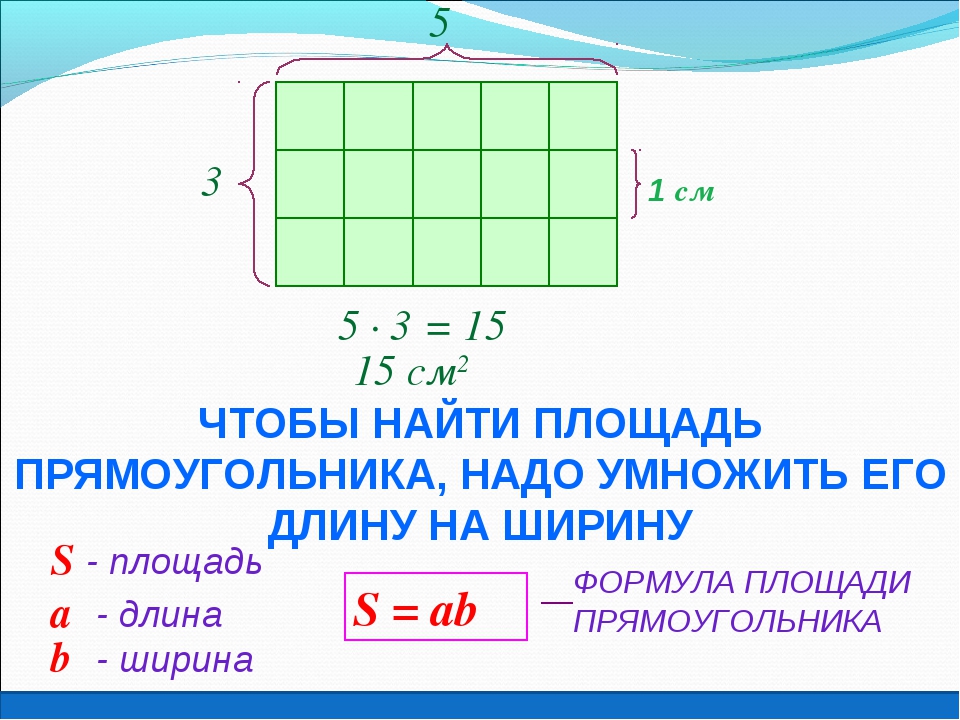
Площадь измеряют в квадратных единицах, миллиметрах, сантиметрах, метрах и так далее. Сколько квадратов в данном прямоугольнике?
Совершенно верно. В нем пятнадцать квадратных единиц. Значит для того,
чтобы найти площадь прямоугольника нужно его ширину умножить на длину.
площадь прямоугольника = ширина х длину.
Вот еще несколько примеров определения площади прямоугольника.
| Площадь = Длина х Ширина Площадь = 9 х 5 = 45 квадратных единиц | |
| Площадь = Длина х Ширина Площадь = 8 х 6 = 48 квадратных единиц |
Единицы измерения площади.
Как было сказано выше площадь измеряется в квадратных единицах. Они
будут различными в зависимости от размера измеряемой площади. Конечно,
можно измерять все в одних единицах, но в результате мы будем получать
либо слишком маленькие, либо слишком большие для восприятия цифры.
| Пример | Единица измерения | Единица площади |
| Ноготь на пальце | Миллиметр | мм2 |
| Лист бумаги | Сантиметр | см2 |
| Комната | Метр | м2 |
| Город | Километр | км2 |
Площадь земельных участков еще часто указывают в сотках.
| Ширина 15, длина 100 | Площадь 1500 м2 | Площадь 15 соток |
| Ширина 20, длина 75 | Площадь 1500 м2 | Площадь 15 соток |
| Ширина 25, длина 60 | Площадь 1500 м2 | Площадь 15 соток |
| ширина 30, длина 50 | Площадь 1500 м2 | Площадь 15 соток |
В будущем, если вы вдруг забудете как найти площадь прямоугольника, то вспоминайте очень старый анекдот, когда дедушка спрашивает у пятиклассника как найти площадь Ленина, а тот отвечает что нужно ширину Ленина умножить на длину Ленина.
Иногда в быту людям приходится вспоминать давно забытые школьные знания.
 Например, когда при очередном ремонте в доме или квартире нужно
определить количество материала для какой-то поверхности треугольной
формы. Когда-то вы знали это на зубок, но теперь судорожно пытаетесь
вспомнить как найти площадь треугольника?
Например, когда при очередном ремонте в доме или квартире нужно
определить количество материала для какой-то поверхности треугольной
формы. Когда-то вы знали это на зубок, но теперь судорожно пытаетесь
вспомнить как найти площадь треугольника?Не переживайте! Это нормально, когда человеческий мозг перекладывает уже давно не используемую информацию в удаленные уголки, из которых ее не вседа получается быстро извлечь. А чтобы вы не мучились этим вопросом, мы напомним как найти площадь треугольника различными методами в данной статье.
Как известно, треугольником называется плоская фигура, образованная пересекающимися прямыми. Точки пересечения называют вершинами, а противоположные им отрезки прямых ребрами. Встречаются частные виды треугольников, такие как прямоугольный, равнобедренный и равносторонний треугольники.
С самом общем случае площадь треугольника находится как половина
произведения длина основания треугольника на величину высоты, опущенной
на данное основание с противоположной вершины.
Данную формулу можно хорошо понять, запомнить и вспоминать по частному случаю нахождения площади прямоугольного треугольника. Посмотрите внимательно на рисунок.
Как видите площадь такого треугольника легко определяется как половина площади воображаемого прямоугольника образованного из двух таких треугольников. Для непрямоугольного треугольника вы как бы добавляете два треугольника до образования прямоугольника и находите его площадь.

Существуют также другие формулы того, как найти площадь треугольника, но мы не станем их здесь приводить, так как в них используются такие данные как синусы углов и которые больше подходят для задач по математической практике, чем по бытовому использованию.
Как найти площадь трапеции? Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде
равнобедренной (равнобокой) трапеции, у которой длина боковых сторон
одинаковы и прямоугольной трапеции, у которой одна из сторон образует с
основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее
основания равна 90, то длина отрезка, соединяющего середины оснований,
равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот.
Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной
трапеции будет перпендикулярен ее основаниям и представляет собой ось
симетрии.
Как найти площадь трапеции.
Площадь трапеции будет равна полусумме ее оснований, умноженной на
высоту. В виде формулы это записывается как S = ((a+b)*h)/2, где
S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота
трапеции.
В виде формулы это записывается как S = ((a+b)*h)/2, где
S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота
трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней
площадь трапеции равна произведению ее средней линии на высоту трапеции и
записывается в виде: S = m*h, где S-площадь, m-длина средней линии,
h-высота трапеции. Данная формула больше подходит для задач по
математике, чем для бытовых задач, так как в реальных условиях вам не
будет известна длина средней линии без предварительных расчетов. А
известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле: S = ((a+b)/2)*√c2-((b-a)2+c2-d2/2(b-a))2, где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Мы знаем, что окружность представляет собой множество точек равноудаленных от заданной точки и лежащих с данной точкой, а также между собой в одной плоскости. Точка, от которой равноудалены другие точки называется центром окружности.
Расстояние от любой точки окружности до его центра называется радиусом окружности и обычно обозначается заглавной английской буквой R.
Расстояние между двумя противолежащими точками, у которых соединяющий их отрезок проходит через центр окружности, называется диаметром окружности и по общепринятым стандартам обозначается английской заглавной буквой D.
Кругом называется часть плосткости, ограниченная окружностью.
Исходя из определения окружности можно понять, что диаметр равен двум радиусм окружности D=2R, а радиус наоборот равен половине диаметра R=D/2.
После того, как были определены все свойства и ключевые характеристики кругов и окружностей можно приступить к определению площади круга, для чего может быть использована следующая формула:
S = πR2
где, S — площадь круга, π — число пи (о нем мы расскажем ниже), R — радиус окружности.
π=3,14.
Формулу площади круга можно преобразовать с учетом того, что радиус равен полудиаметру круга. В этом случае она примет вид:
D = πD2/4
где, S — площадь круга, π — число пи, D — диаметр окружности.
Площадь прямоугольника способы. Как узнать площадь прямоугольника
Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°.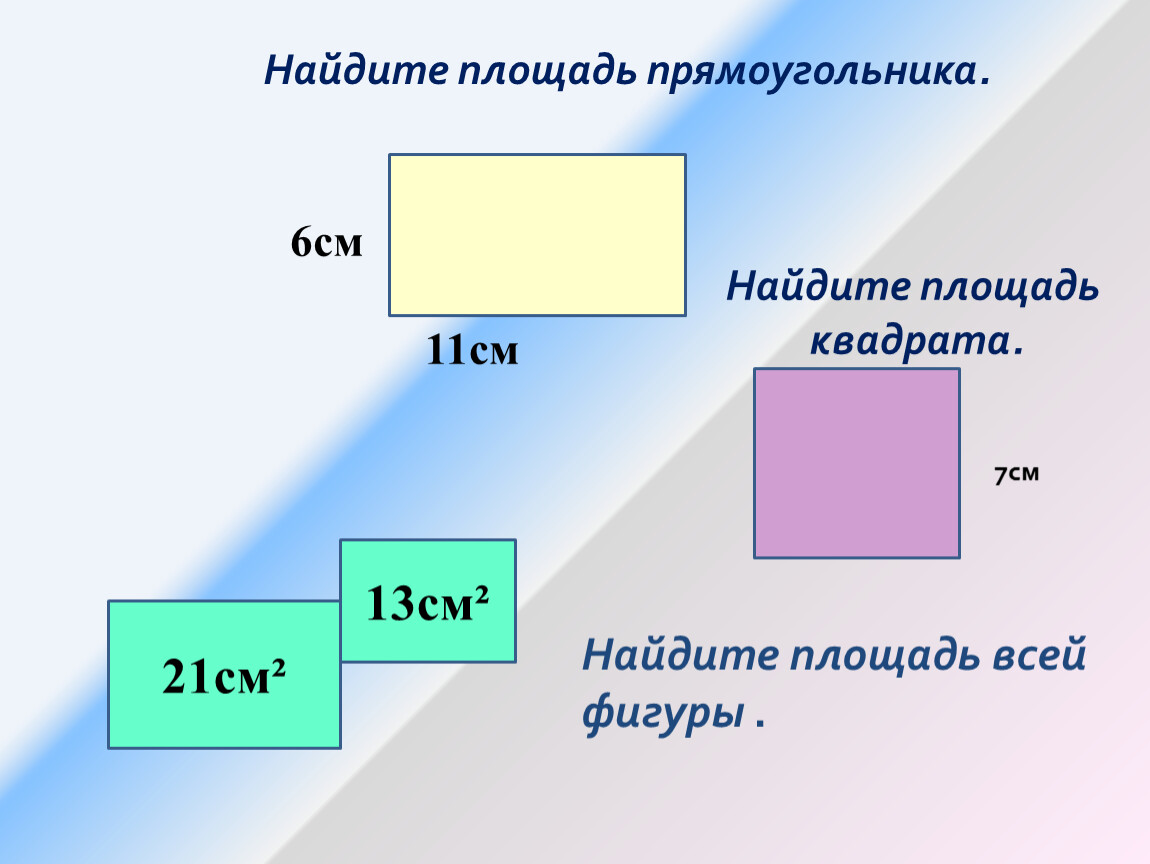 Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Площадь квадрата и как ее найти
Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a 2 , где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.
Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.
Как найти периметр квадратаПериметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.
Пример:
- сторона квадрата = 5, следовательно, P = 4*5 = 20
- сторона квадрата = 3, следовательно, Р = 4*3 = 12
Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.
При решении нужны формулы, которые представлены ранее.
Например: как найти периметр квадрата, если известна площадь, равная 144?
Шаги решения:
- Выясняем длину одной стороны: а = √144 = 12
- Находим периметр: Р = 4*12 = 48.
Нахождение периметра вписанного квадрата
Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Алгоритм решения:
- так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
- затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
- делим уравнение на 2: (a 2 ) = 2(r) 2 ;
- извлекаем корень: a = √(2r).
В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).
- Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).

Задача:
Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a
2
) = 10
2
, то есть 2a
2
= 100. Делим полученное на два и в результате: a
2
= 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Рассмотрим еще один вопрос
Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?
Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см
2
, найдите его периметр.
Шаги решения:
- Находим сторону квадрата: а = √25 = 5.
- Находим сам периметр: Р = 4*а = 4*5 = 20.
Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.
Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.
Мы уже познакомились с понятием площадь фигуры , узнали одну из единиц измерения площади — квадратный сантиметр . На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см 2 .
Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .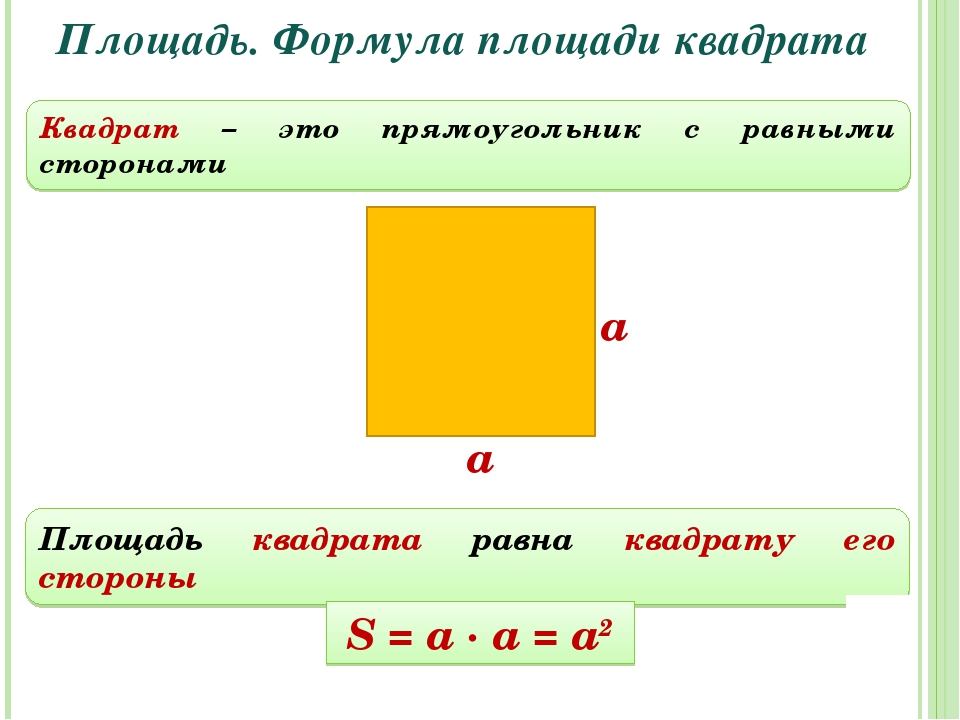
Тогда площадь прямоугольника будет равна 4*3=12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
Ответ: площадь прямоугольника 18см 2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так. Поскольку площадь — это произведение длин сторон прямоугольника, поэтому надо вспомнить таблицу умножения. При умножении каких чисел получается ответ 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Решите задачу.
Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.
Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.
Запишем решение.
Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решите задачу.
Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)
Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.
Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника.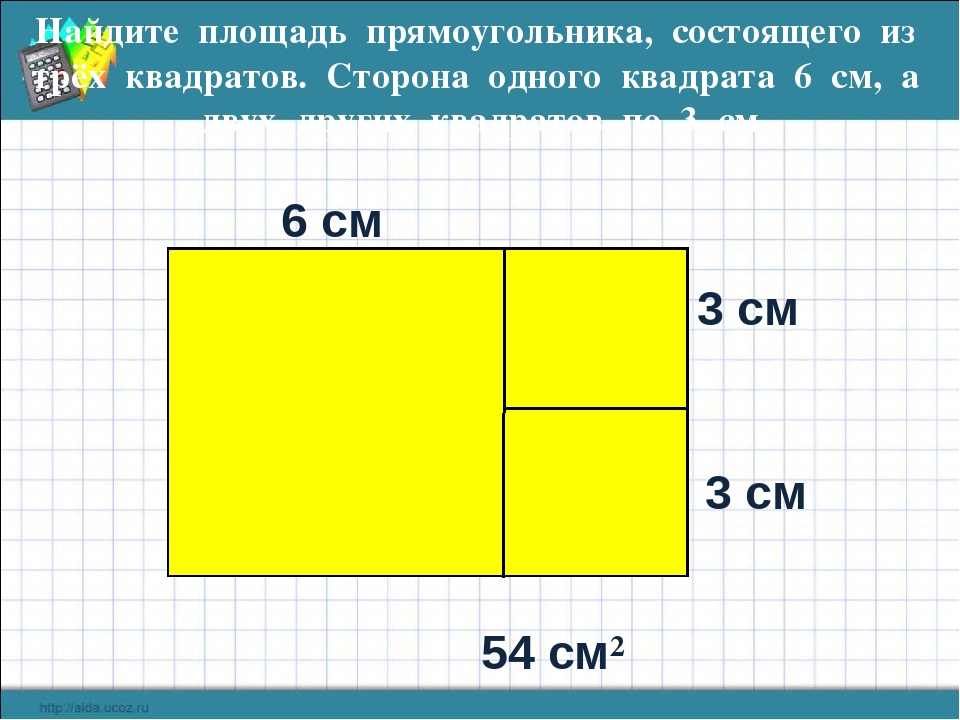 Значит, надо 12 уменьшить в 2 раза.
Значит, надо 12 уменьшить в 2 раза.
Ответ: площадь треугольника 6 см 2 .
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.
1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.
2. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .
4. Составьте задание по теме урока для своих товарищей.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
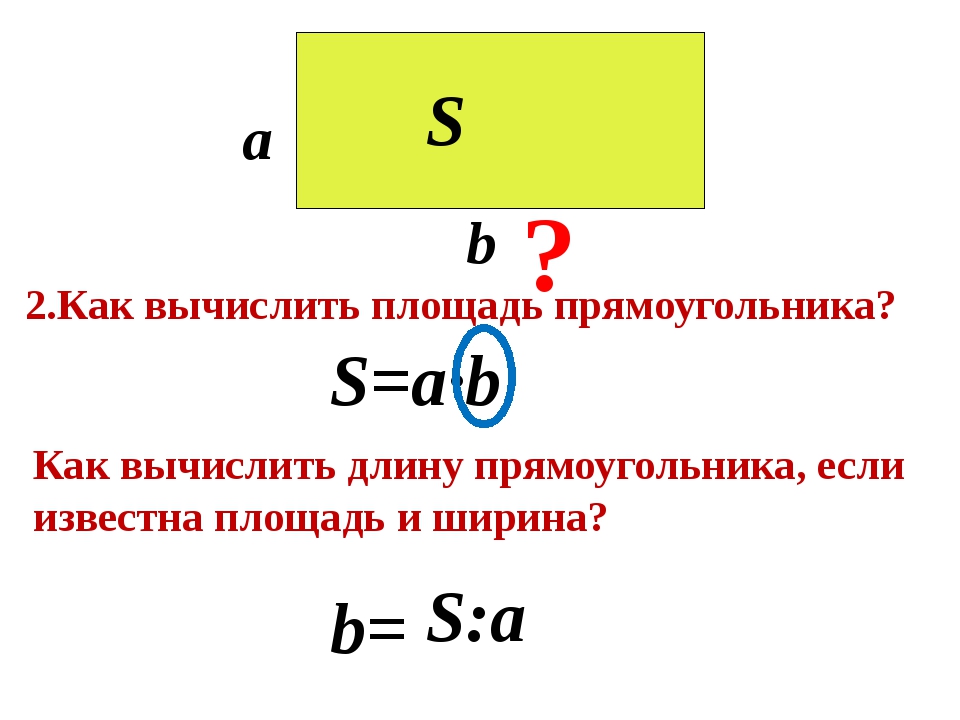
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
Запиши ответ в квадратных сантиметрах.2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника, используя длину диагонали и одну из сторон. 2$.
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 292.
Как найти площадь, периметр прямоугольника и квадрата: формулы / 01.11.2021
Если вам необходимо вычислить площадь прямоугольника или квадрата, воспользуйтесь нашим пошаговым путеводителем. Prostobank.ua рассказывает, как узнать площадь прямоугольника или квадрата.

Что такое прямоугольник и квадрат?
Прямоугольник – это четырехугольник, у которого все углы прямые (равны 90 градусам). Прямоугольник, у которого все стороны равны, называется квадратом.
Стороны прямоугольника обозначаются латинскими буквами a (ширина) и b (длина), стороны квадрата – a
Формула расчета площади прямоугольника
Для того чтобы рассчитать площадь прямоугольника (S), необходимо его длину умножить на ширину.
Sпрямоугольника=а*b
Формула расчета площади квадрата
Для того чтобы рассчитать площадь квадрата (S), необходимо его длину умножить на ширину.
Sквадрата=а*a=a2
Поскольку диагонали квадрата равны, пересекаются под прямым углом, и точкой пересечения делятся пополам и являются биссектрисами его углов, вычислить площадь квадрата можно также по такой формуле:
Sквадрата=d2/2, где d – длина диагонали квадрата.
Как видно из вышеописанных формул, посчитать площадь прямоугольника или квадрата достаточно просто. Если вам необходимо перевести площадь из квадратных сантиметров в квадратные метры воспользуйтесь нашим калькулятором площади.
Как найти периметр прямоугольника?
Периметр прямоугольника – это сумма всех его сторон. Поэтому Pпрямоугольника=2*(a+b), где a –ширина, b длина
Как найти площадь квадрата, если известен периметр?
Периметр квадрата (Pквадрата) = 4*a, где a – сторона квадрата
Если нам известен периметр квадрата, поэтому сторона квадрата равна: a=P/4
Sквадрата=a2=( P/4)2
Как мы находим площадь. Как найти площадь прямоугольника
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см.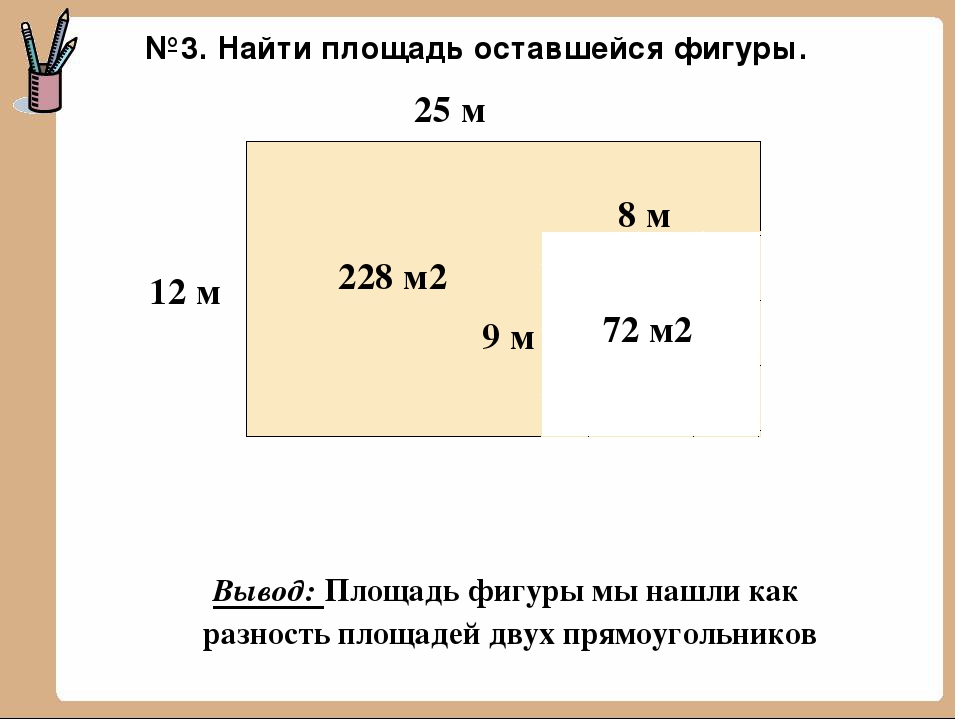 Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника, используя длину диагонали и одну из сторон. Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Следовательно, можно определить вторую сторону прямоугольника, воспользовавшись теоремой Пифагора. После этого задача сводится к предыдущему пункту.
Как узнать площадь прямоугольника по периметру и стороне
Периметр прямоугольника – это сумма всех его сторон. Если известен периметр прямоугольника и одна сторона (например ширина), можно вычислить площадь прямоугольника, воспользовавшись следующей формулой:
Площадь = (Периметр×ширина – ширина^2)/2.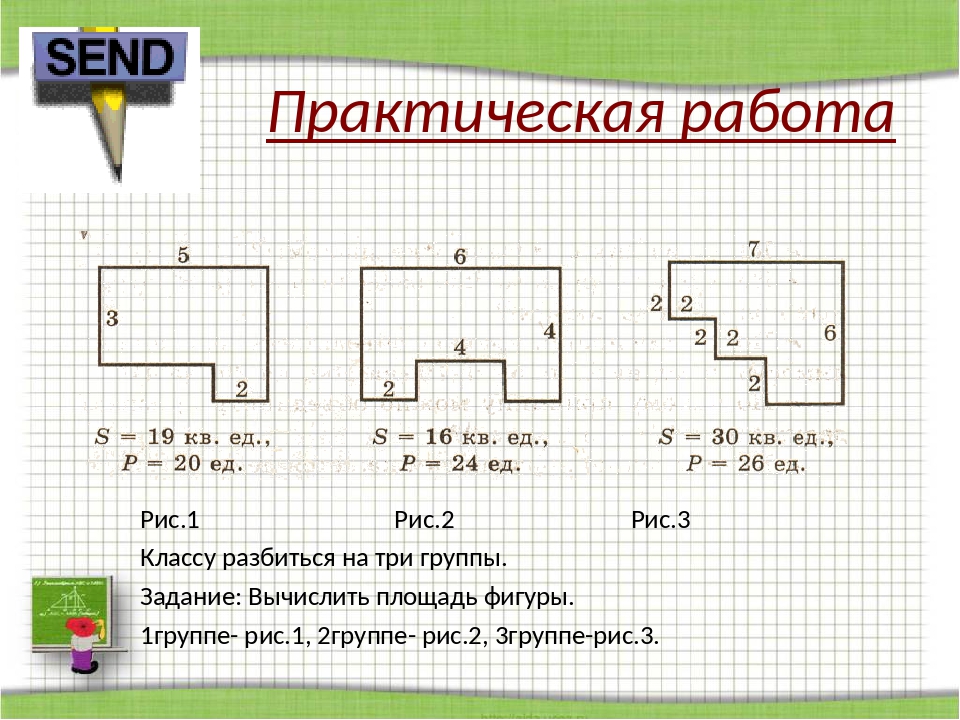 2 × sin(острого угла между диагоналями)/2.
2 × sin(острого угла между диагоналями)/2.
Одна из первых формул, которая изучается в математике, связана с тем, прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.
Какие единицы измерения площади существуют?
Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.
Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.
При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.
Как быть, если заданы стороны прямоугольника?
Подобным образом рассчитывается который является частным случаем прямоугольника.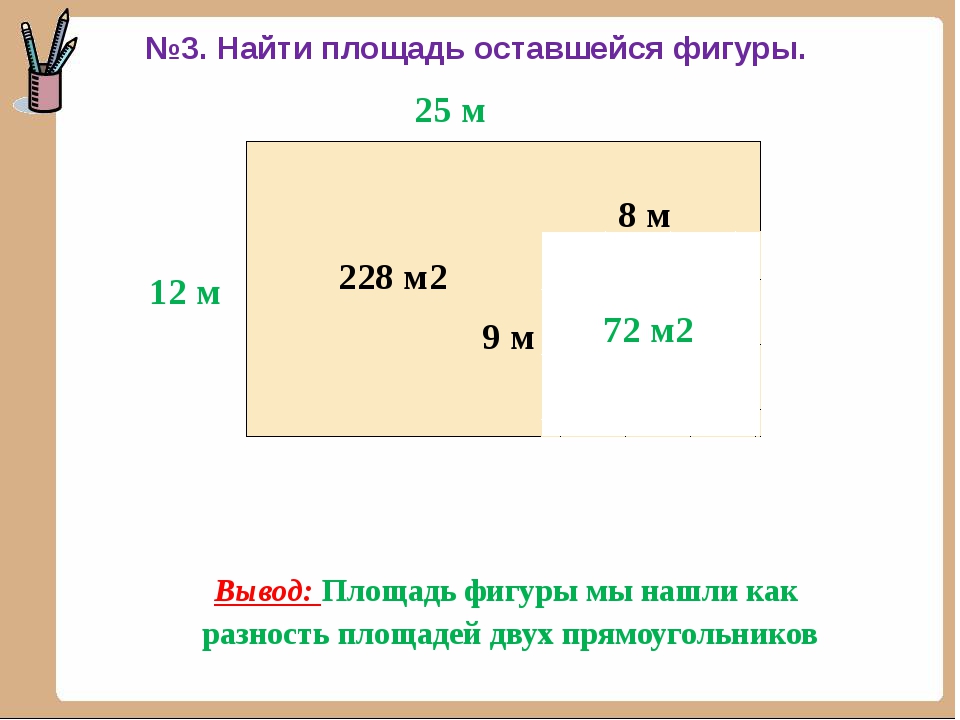 Так как у него все стороны равны, то произведение становится квадратом буквы а .
Так как у него все стороны равны, то произведение становится квадратом буквы а .
Как быть, если фигура изображена на клетчатой бумаге?
В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника. Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.
Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.
Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех А их четыре. К слову, их рассчитывают как половину произведения катетов.
Итоговый результат даст значение площади данного прямоугольника.
Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?
До того в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой.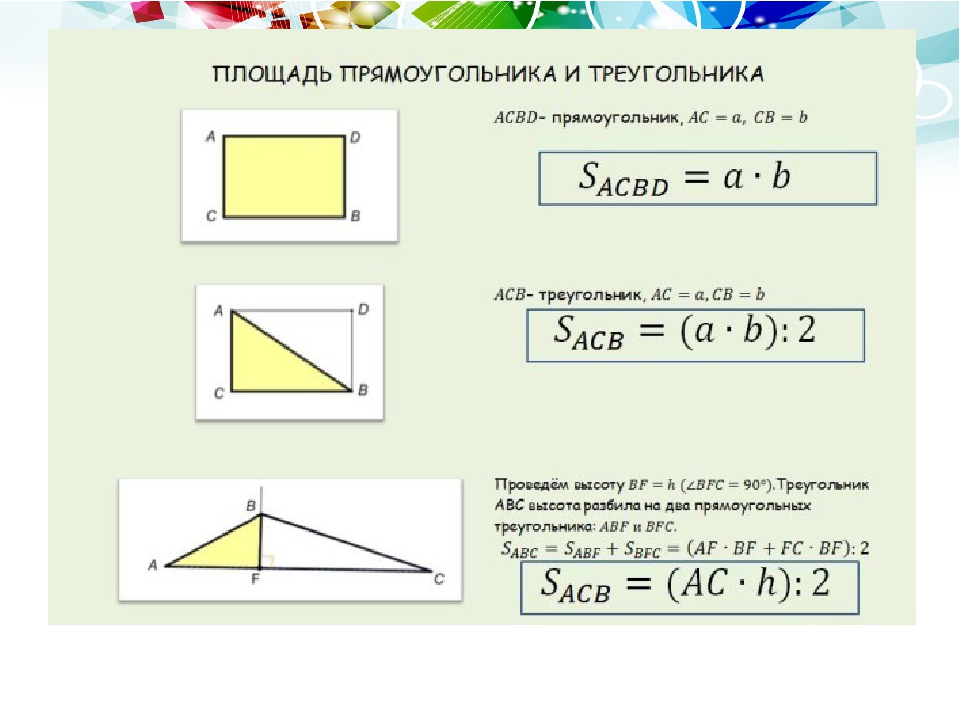 Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.
Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.
Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться
Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.
Что делать, если в задаче дан периметр?
Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.
Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины.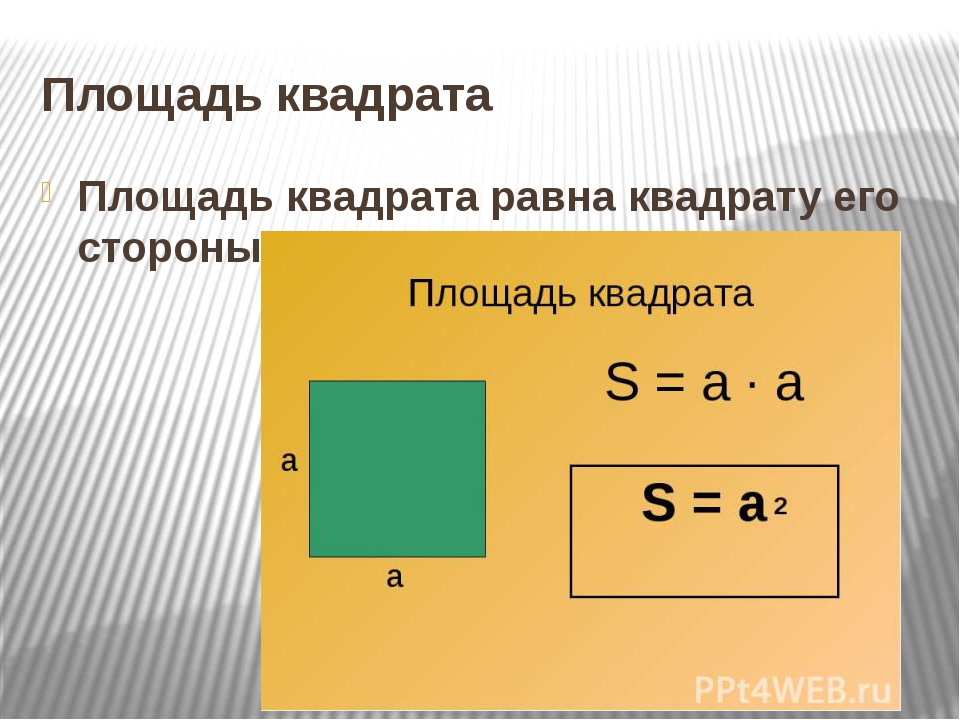 Необходимо узнать его площадь.
Необходимо узнать его площадь.
Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.
Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.
Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.
Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см 2 . Последнее число — ответ рассмотренной задачи.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны.
 А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два.
 Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Инструкция
Например, вам , что длина одной из сторон (а) равна 7 см, а периметр прямоугольника (P) равен 20 см.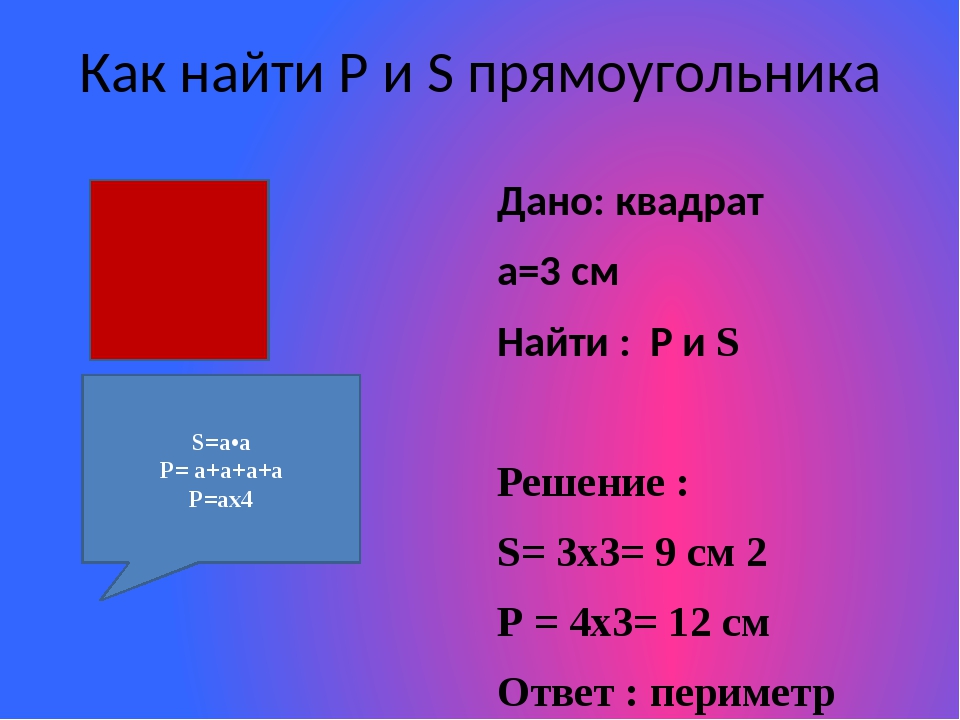 Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Теперь, зная длины обеих смежных сторон (a и b), вы сможете подставить их в формулу площади S = ab. В данном случае прямоугольника будет равна 7х3 = 21. Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.
Источники:
- как находится периметр прямоугольника
Плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника приходится вычислять чаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.
Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.
Инструкция
Кстати, из прямоугольника можно легко вычислить площадь . Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.
Видео по теме
Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Инструкция
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.д.
Инструкция
Если известна величина угла (α), который составляет диагональ прямоугольника с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических в прямоугольном . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла.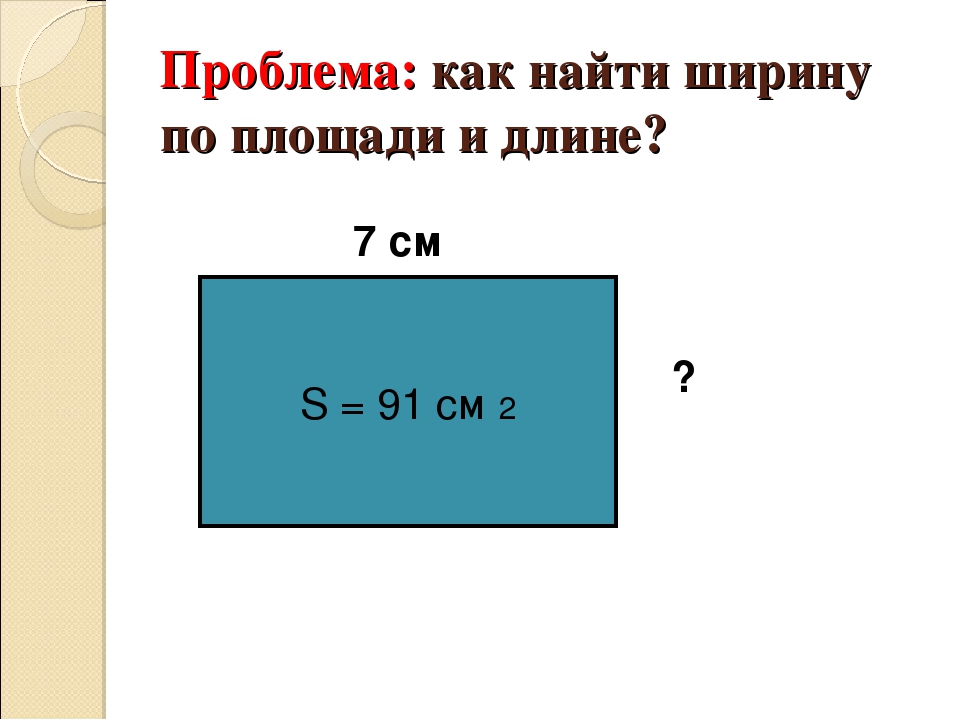 Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².
Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².
Если кроме длины диагонали (С) прямоугольника известна величина угла (β), который образуют диагонали, то для вычисления площади фигуры можно тоже задействовать одну из тригонометрических функций — синус. Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.
Если известен (r) вписанной в прямоугольник окружности, то для вычисления площади возведите эту величину во вторую степень и увеличьте результат в четыре раза: S=4*r². Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.
Если известны длины (P) и одной из сторон (A) прямоугольника , то для нахождения площади внутри этого периметра вычислите половину произведения длины стороны на разницу между длиной периметра и двумя длинами этой стороны: S=A*(P-2*A)/2.
Видео по теме
С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы огородить его забором? Так знания основ геометрии иногда незаменимы для осуществления важных проектов.
Найти стороны прямоугольника известна только площадь. Периметр и площадь прямоугольника
Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко
мнаты и другое.
Геометрическая фигура
Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной.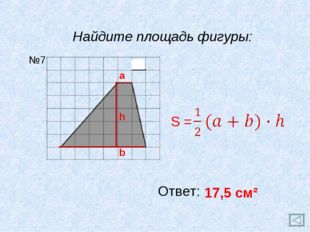 Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.
Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.
Площадь=длина*ширина
Но еще одна оговорка: длина и ширина должны быть выражены в одинаковых единицах измерения, то есть метр и метр, а не метр и сантиметр. Записывается площадь латинской буквой S. Для удобства обозначим длину латинской буквой b, а ширину латинской буквой a, как показано на рисунке. Отсюда мы делаем вывод, что единицей измерения площади является мм 2 , см 2 , м 2 и т. д.
Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед 2 . Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. S стены 1 =5,5*3,
S стены 1 =16,5 м 2 . Следовательно, противоположная стена имеет площадь равную 16,5 м 2 . Найдем площади следующих двух стен. Стороны их, соответственно, равны 3,5 м и 3 м. S стены 2 =3,5*3, S стены 2 =10,5 м 2 . Значит, и противоположная сторона равна 10,5 м 2 . Сложим все результаты. 16,5+16,5+10,5+10,5=54 м 2 . Как вычислить площадь прямоугольника, если стороны выражены в разных единицах измерения. Ранее мы вычисляли площади в м 2 , то и в этом случае будем использовать метры. Тогда ширина рулона обоев будет равна 0,5 м. S рулона =10*0,5, S рулона =5 м 2 . Теперь узнаем, сколько рулонов необходимо для оклейки комнаты. 54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев. Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .
Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .
Резюме
Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.
4. Формула радиуса окружности, которая описана около прямоугольника через диагональ квадрата :
5. Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):
6. Формула радиуса окружности, которая описана около прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:
Формула радиуса окружности, которая описана около прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:
7. Формула радиуса окружности, которая описана около прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны у этого угла:
8. Формула радиуса окружности, которая описана около прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника.
Формулы для определения угла между стороной и диагональю прямоугольника:
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника.
Формулы для определения угла меж диагоналей прямоугольника:
1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:
β = 2α
2.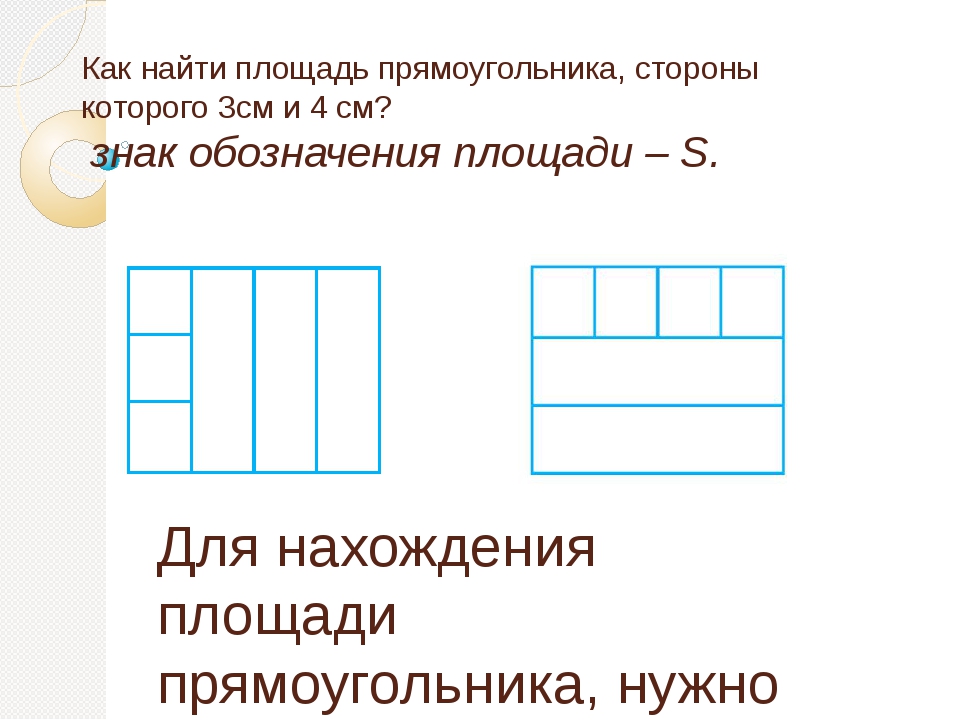 Формула определения угла между диагоналями прямоугольника через площадь и диагональ.
Формула определения угла между диагоналями прямоугольника через площадь и диагональ.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали.
 В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений.
 Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Определение.
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника , а короткую — шириной прямоугольника .
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.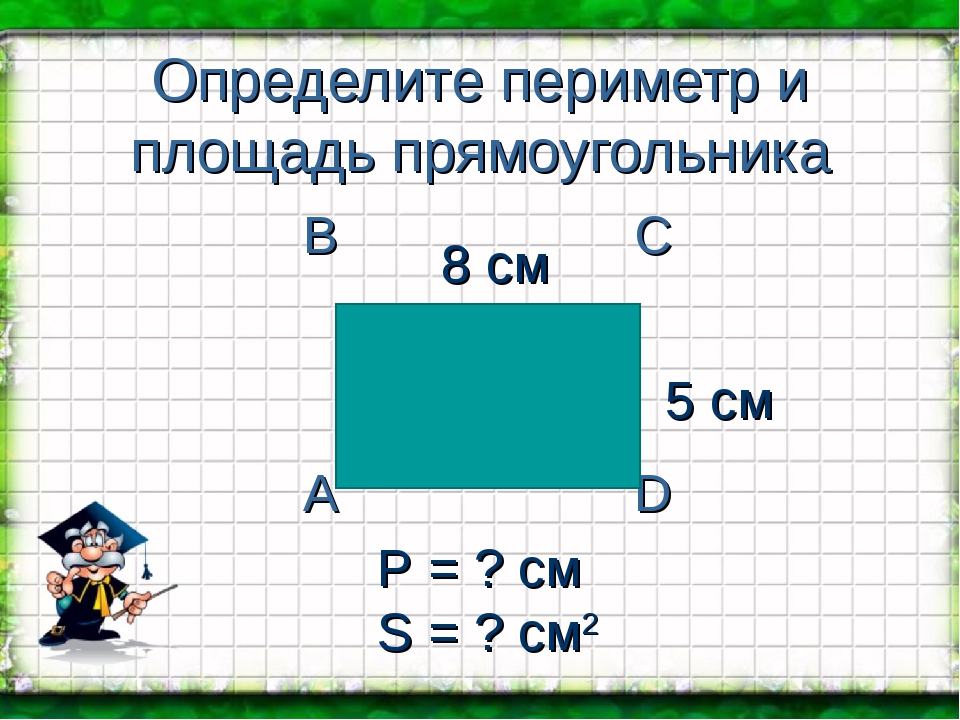
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d 2 — b 2
b = √d 2 — a 2
2.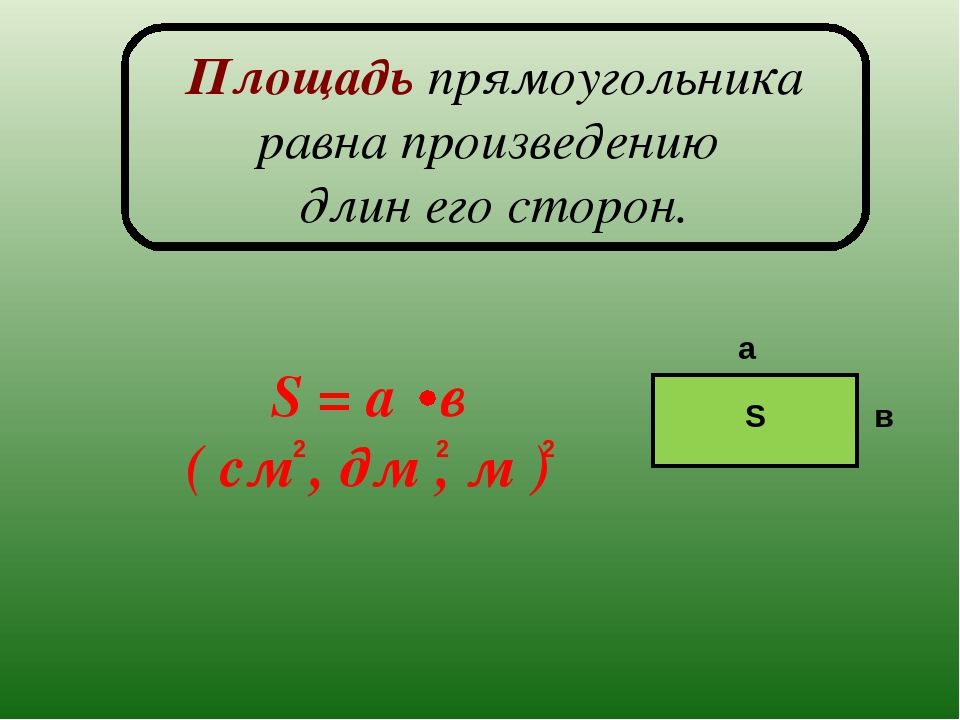 Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a 2 + b 2
2. Формула диагонали прямоугольника через площадь и любую сторону:
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = D о
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S: sin β
Периметр прямоугольника
Определение.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b )
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a 2 | = | 2S + 2b 2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d 2 — a 2 ) = 2(b + √d 2 — b 2 )
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R 2 — a 2 ) = 2(b + √4R 2 — b 2 )
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √D o 2 — a 2 ) = 2(b + √D o 2 — b 2 )
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.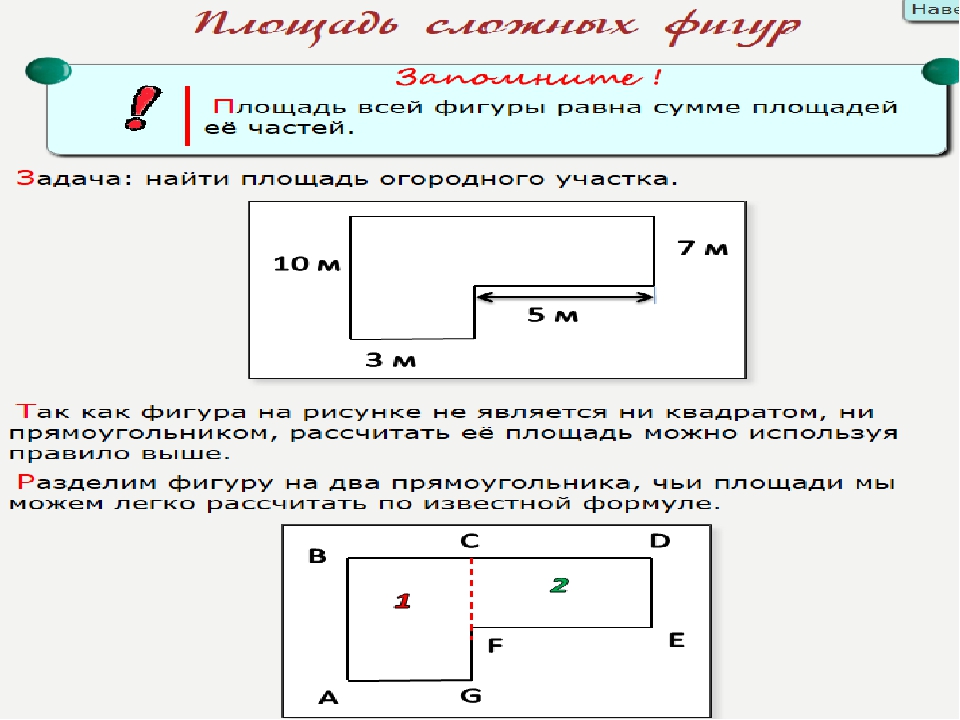
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a √4R 2 — a 2 = b √4R 2 — b 2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a √D o 2 — a 2 = b √D o 2 — b 2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
4a, где a — сторона квадрата или ромба. Тогда длина стороны равна одной четвертой периметра: a = p/4. 1/2)/2. Отбросьте тот корень, который будет меньше ноля, и подставьте в для стороны a.
1/2)/2. Отбросьте тот корень, который будет меньше ноля, и подставьте в для стороны a.
Источники:
- Найти стороны прямоугольника
Если вы знаете значение а, то вы можете сказать, что решили квадратное уравнение, потому как его корни будут найдены очень легко.
Вам понадобится
- -формула дискриминанта квадратного уравнения;
- -знание таблицы умножения
Инструкция
Видео по теме
Полезный совет
Дискриминант квадртаного уравнения может быть положительным, отрицательным, или равняться 0.
Источники:
Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Инструкция
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще.
Вам понадобится
- калькулятор, линейка
Инструкция
Чтобы измерьте длину одной из его сторон и умножьте результат измерения на три. В виде это можно записать следующим образом:
Прт = Дс * 3,
Прт – периметр треугольника,
Дс – длина любой из его сторон.
Периметр треугольника получится в тех же измерения, что и длина его стороны.
Так как равносторонний треугольник обладает высокой степенью симметрии, то для вычисления его периметра достаточно одного из параметров. Например, площади, высоты, вписанной или описанной окружности.
Если известен радиус вписанной окружности равностороннего треугольника, то для вычисления его периметра воспользуйтесь следующей формулой:
Прт = 6 * √3 * r,
где: r — радиус вписанной окружности. ¼.
¼.
Видео по теме
Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон одинаковой длины и четырех прямых углов, каждый из которых равен 90°. Определение площади или периметра четырехугольника, причем любого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти умения могут стать полезными, например, во время ремонта при расчете нужного количества материалов — покрытий для пола, стен или потолка, а также для разбивки газонов и грядок и т.д.
Как найти площадь прямоугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Что такое площадь?
Площадь — это размер поверхности!
Пример:
У всех этих фигур одинаковая площадь 9:
Это помогает представить , сколько краски покроет форму.
Площадь простых форм
Для определенных форм существуют специальные формулы:
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = Ш × В
Ш = Ширина
В = Высота
Ширина равна 5, а высота 3, поэтому мы знаем, что w = 5 и h = 3 :
.Площадь = 5 × 3 = 15
Узнайте больше в Area of Plane Shapes.
Площадь по счету квадратов
Мы также можем нанести фигуру на сетку и подсчитать количество квадратов:
Прямоугольник имеет площадь 15
Пример: когда каждый квадрат равен 1 метр со стороны, тогда площадь составляет 15 м 2 (15 квадратных метров)
Квадратный метр vs Квадратный метр
Базовая единица площади в метрической системе — квадратный метр , который представляет собой квадрат с 1 метром на каждой стороне:
1 квадратный метр
Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:
Есть также «квадратный мм», «квадратный см» и т.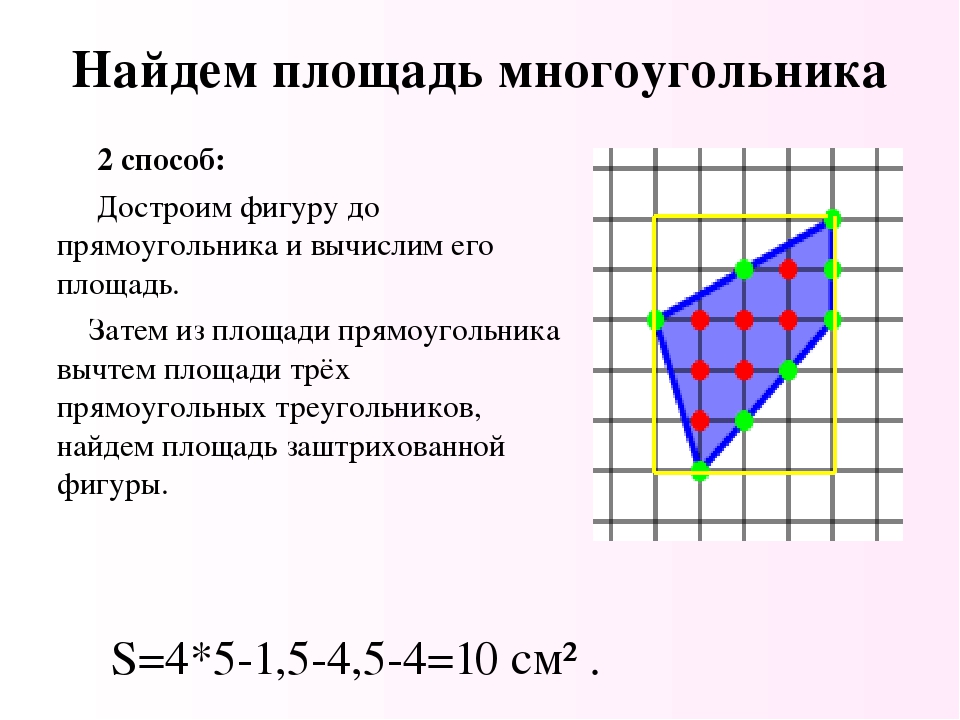 Д., Подробнее см. Метрическая площадь.
Д., Подробнее см. Метрическая площадь.
Примерная площадь по подсчету квадратов
Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.
В одну сторону:
- больше чем половина квадрата считается как 1
- меньше чем половина квадрата считается как 0
Как это:
Этот пятиугольник имеет площадь примерно 17
Или мы можем посчитать один квадрат, когда кажется, что площади
в сумме дают .Пример: Здесь область, обозначенная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):
Этот круг имеет площадь примерно 14
Но лучше всего использовать формулу (когда это возможно):
Пример: круг имеет радиус 2,1 метра:
Формула:
Площадь = π × r 2
Где:
Радиус 2. 1м , итого:
1м , итого:
Площадь = 3,1416 … × (2,1 м) 2
= 3,1416 … × (2,1 м × 2,1 м)
= 13,854 … м 2
Таким образом, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)
Область сложных форм
Иногда мы можем разбить фигуру на две или более простые формы:
Пример: Какова площадь этой фигуры?
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B
Площадь = 400 м 2 + 140 м 2
Площадь = 540м 2
Площадь путем сложения треугольников
Мы также можем разбить фигуру на треугольники:
Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:
Затем рассчитайте каждую площадь
(используя Area = ½b × h) и сложите их все.
Площадь по координатам
Когда мы знаем координаты каждой угловой точки, мы можем использовать метод «Площадь неправильных многоугольников».
Есть область многоугольника с помощью инструмента рисования, который тоже может помочь.
Площадь прямоугольника — формула, определение, примеры
Площадь любой формы — это количество единичных квадратов, которые могут в нее поместиться.Здесь «единица» относится к единице (1), а единичный квадрат — это квадрат со стороной, равной 1 единице. Итак, площадь прямоугольника — это количество единичных квадратов внутри границы прямоугольника. В качестве альтернативы пространство, занимаемое по периметру прямоугольника, называется площадью прямоугольника. Хорошим примером прямоугольной формы являются квадратные плитки единичной длины в вашем доме. Вы легко сможете определить, сколько места занимает пол, посчитав количество плиток. Это также поможет вам определить площадь прямоугольного пола.
Что такое площадь прямоугольника?
Площадь можно определить как объем пространства, занимаемого плоской поверхностью определенной формы. Он измеряется в терминах «количества» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. Д.). Площадь прямоугольника — это количество единичных квадратов, которые могут поместиться в прямоугольник. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов портативных компьютеров, школьные доски, холсты для рисования и т. Д. Вы можете использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами.Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма.
Площадь прямоугольника Определение: Площадь, занимаемая прямоугольником в пределах его границ, называется площадью прямоугольника.
Нарисуем внутри прямоугольника единичные квадраты. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм.
Теперь посчитайте количество единичных квадратов на рисунке выше. Сколько квадратов вы можете наблюдать? Всего 12 квадратов.Мы уже узнали, что площадь измеряется в квадратных единицах. Поскольку единица измерения этого прямоугольника — дюймы, площадь измеряется и записывается в квадратных дюймах. Таким образом, площадь вышеуказанного прямоугольника = 12 квадратных дюймов.
Формула площади прямоугольника
Формула площади прямоугольника используется для определения площади, занимаемой прямоугольником в пределах его границ. В приведенном выше примере площадь прямоугольника, длина которого составляет 4 дюйма, а ширина — 3 дюйма, составляет 12 квадратных дюймов.У нас 4 × 3 = 12. Площадь прямоугольника получается умножением его длины и ширины. Таким образом, формула для площади «A» прямоугольника, длина и ширина которого равны «l» и «w» соответственно, представляет собой произведение « l × w ».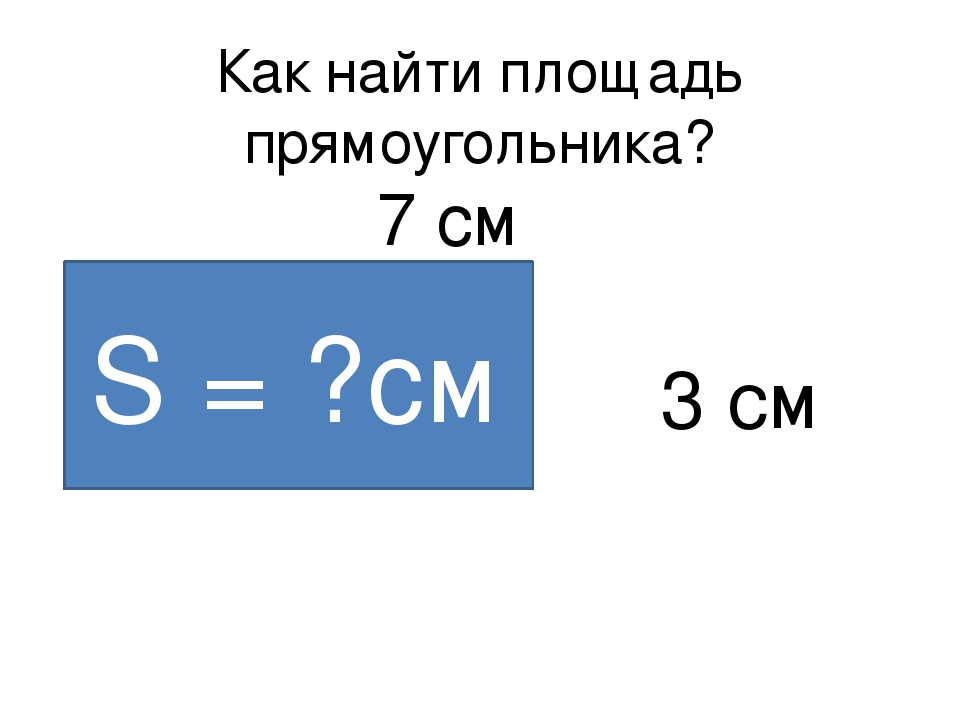
Площадь прямоугольника = (длина × ширина) квадратных единиц
Как рассчитать площадь прямоугольника?
Площадь прямоугольника равна его длине, умноженной на ширину. Следуйте инструкциям ниже, чтобы найти площадь прямоугольника.
- Шаг 1 : Обратите внимание на размеры длины и ширины из приведенных данных.
- Шаг 2 : Найдите произведение значений длины и ширины.
- Шаг 3 : Ответьте в квадратных единицах.
Давайте рассмотрим пример вычисления площади прямоугольника. Найдем площадь прямоугольника, длина которого составляет 15 единиц, а ширина — 4 единицы. Чтобы найти площадь, сначала найдите длину и ширину.
Дано, длина = 15 единиц и ширина = 4 единицы
Формула для определения площади прямоугольника: A = l × w. Замените 15 вместо l и 4 вместо w в этой формуле. Площадь прямоугольника = 15 × 4 = 60.
Следовательно, площадь прямоугольника = 60 квадратных единиц
Площадь прямоугольника по диагонали
Диагональ прямоугольника — это прямая линия в прямоугольнике, соединяющая его противоположные вершины. В прямоугольнике две диагонали, обе одинаковой длины.Мы можем найти диагональ прямоугольника, используя теорему Пифагора.
В прямоугольнике две диагонали, обе одинаковой длины.Мы можем найти диагональ прямоугольника, используя теорему Пифагора.
(диагональ) 2 = (длина) 2 + (ширина) 2
(длина) 2 = (диагональ) 2 — (ширина) 2
Длина = ⎷ (диагональ) 2 — (ширина) 2
Теперь формула для вычисления площади прямоугольника — длина × ширина. В качестве альтернативы мы можем записать этот продукт как (⎷ (Диагональ) 2 — (Ширина) 2 ) × Ширина
Итак, площадь прямоугольника = ширина (⎷ (диагональ) 2 — (ширина) 2 )
Почему площадь прямоугольника равна длине × ширине?
Вы когда-нибудь задумывались, почему формула для определения площади прямоугольника равна длине × ширине? Выведем формулу площади прямоугольника.Нарисуем диагональ AC в прямоугольнике ABCD. Ясно, что диагональ AC делит прямоугольник ABCD на два равных треугольника. Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника ABCD = Площадь треугольника ABC + Площадь треугольника ADC
= 2 × Площадь треугольника ABC
= 2 × (1/2 × основание × высота)
= AB × BC
= длина × ширина
Часто задаваемые вопросы о площади прямоугольника
Какова площадь прямоугольника в геометрии?
Площадь пространства, занимаемого по периметру прямоугольника, называется площадью прямоугольника.Он рассчитывается путем нахождения произведения длины и ширины прямоугольника.
Каков периметр и площадь прямоугольника?
Периметр прямоугольника равен сумме его четырех сторон. Следовательно, периметр прямоугольника = 2 единицы (длина + ширина). Площадь прямоугольника определяется как произведение длины и ширины. Выражается в квадратных единицах.
Какова формула площади прямоугольника?
Площадь прямоугольника (A) равна произведению его длины «a» и ширины или ширины «b».Итак, площадь прямоугольника = (a × b) квадратных единиц.
Какова единица площади прямоугольника?
Единица площади прямоугольника — квадратные единицы. Например, если размеры прямоугольника 4 дюйма × 3 дюйма. Площадь прямоугольника 12 квадратных дюймов.
Почему мы вычисляем площадь прямоугольника?
Мы вычисляем площадь прямоугольника, чтобы найти площадь, занимаемую прямоугольником в пределах его периметра.
Как определить площадь прямоугольника по его диагонали?
Мы можем найти диагональ прямоугольника, используя теорему Пифагора: (Диагональ) 2 = (Длина) 2 + (Ширина) 2 .Теперь формула для вычисления площади прямоугольника — длина × ширина. В качестве альтернативы мы можем записать этот продукт как (⎷ (Диагональ) 2 — (Ширина) 2 ) × Ширина
Площадь прямоугольника такая же, как и площадь квадрата?
Нет, площадь квадрата не обязательно совпадает с площадью прямоугольника, потому что каждый квадрат представляет собой прямоугольник с равной длиной и шириной, но все прямоугольники не квадратные. Формула для вычисления площади прямоугольника — длина × ширина, а площадь квадрата — (сторона) 2 .
Площадь прямоугольников — объяснения и примеры
По определению, площадь прямоугольника — это область, охватываемая прямоугольником в двухмерной плоскости . Прямоугольник — это двумерный многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вершинами.
Прямоугольник состоит из двух сторон: длины (L) и ширины (W). Длина прямоугольника — самая длинная сторона, а ширина — самая короткая. Ширина прямоугольника иногда обозначается как ширина (b).
Как найти площадь прямоугольника?
Площадь прямоугольника можно рассчитать, подсчитав количество маленьких полных квадратов размером 1 * 1 кв. Единиц, необходимых для покрытия прямоугольника.
Например, если количество подсчитанных полных квадратов равно 20, это означает, что площадь прямоугольника равна 20 единицам квадратов.
Недостаток этого метода заключается в том, что он не дает точных значений площади, а также метод неприменим для определения площади больших плоскостей.
Площадь прямоугольника Формула
Площадь прямоугольника равна произведению ширины и длины прямоугольника.
Следовательно, формула площади прямоугольника утверждает, что:
Площадь прямоугольника = Длина x Ширина
A = L * W, где A — площадь, L — длина, W — ширина или ширина .
ПРИМЕЧАНИЕ: При умножении длины на ширину всегда проверяйте, что вы работаете в одной и той же единице длины. Если они даны в разных единицах, замените их на одну и ту же единицу.
Давайте решим несколько примеров задач о площади прямоугольника.
Пример 1
Найдите площадь прямоугольника, если его длина 25 м, а ширина 10 м.
Раствор
A = l x w
Заменить 25 на l и 10 на w.
= (25 x 10) м 2
= 250 м 2
Итак, площадь прямоугольника 250 м 2 .
Пример 2
Найдите площадь прямоугольника, длина и ширина которого составляют 10 см и 3 см соответственно.
Раствор
Дано,
Длина (l) = 10 см.
Ширина (б) = 3 см.
Площадь прямоугольника = длина × ширина
= 10 × 3 см 2 .
= 30 см 2 .
Пример 3
Если периметр прямоугольника составляет 60 см, а его длина в 5 раз больше ширины, найдите площадь прямоугольника.
Решение
Пусть ширина будет x.
Длина в 5 раз больше ширины, длина = 5x.
Но периметр прямоугольника = 2 (l + w) = 60 см.
Замените 5x вместо l и x вместо w.
60 = 2 (5x + x)
60 = 12x
Разделите обе стороны на 12, чтобы получить.
x = 5
Теперь подставьте x = 5 в уравнение длины и ширины.
Следовательно, ширина = 5 см, а длина = 25 см.
Но площадь прямоугольника = lxw
= (25 x 5) см 2
= 125 см 2
Пример 4
Найдите площадь прямоугольника длиной 12 см и диагональ 13 см.
Решение
Здесь ширина не указана, поэтому мы используем теорему Пифагора для определения ширины.
c 2 = a 2 + b 2
13 2 = a 2 + 12 2
169 = a 2 + 144.
Вычесть 144 с обеих сторон .
169 — 144 = a 2 + 144 — 144
25 = a 2
Найдя квадратный корень из обеих частей, мы получим.
a = 5
Следовательно, ширина прямоугольника 5 см.
Теперь посчитайте площадь.
A = Д x Ш
= (12 x 5) см 2
Пример 5
Если цена цементирования пола составляет 12,40 долларов США за квадратный метр, найдите стоимость цементирования прямоугольного пола длиной 20 м и шириной 10 м.
Раствор
Чтобы найти общую стоимость цементирования пола, умножьте площадь пола на коэффициент цементирования.
Площадь = Д x Ш
= (20 x 10) м 2
= 200 м 2
Стоимость цементирования = площадь x скорость цементирования
= 200 м 2 x 12,40 долл. США / м 2
= 2480 долларов США
Пример 6
Длина и ширина находятся в соотношении 11: 7, а его площадь составляет 693 квадратных фута. Найдите его длину и ширину.
Решение
Пусть общее соотношение длины и ширины = x
Следовательно, длина = 11x
Ширина = 7x
Площадь прямоугольника = L x W
693 кв.футов = (11x) (7x)
693 кв. ft = 77x 2
Разделим обе стороны на 77.
x 2 = 9
Найдите квадрат обеих сторон, чтобы получить;
x = 3.
Заменитель.
Длина = 11x = 11 * 3 = 33
Ширина = 7x = 7 * 3 = 21
Следовательно, длина прямоугольника составляет 33 фута, а его ширина — 21 фут.
Пример 7
Длина прямоугольника 0,7 м, ширина 50 см.Какова площадь прямоугольника в метрах?
Раствор
Длина = 0,7 м
Ширина = 50 см.
Преобразуйте 50 см в метры, разделив 50 на 100. Итак, 50 см = 0,5 м
Площадь = Д x Ш
= (0,7 x 0,5) м 2
= 0,35 м 2
Пример 8
Размер прямоугольной стены 75 м на 32 м. Узнайте стоимость покраски стены, если ставка покраски 5 рупий за кв.м.
Раствор
Площадь = Д x Ш
= (75 x 32) м 2
= 2400 м 2
Чтобы получить стоимость покраски стены, умножаем площадь стены по скорости покраски.
Стоимость = 2400 м 2 x 5 рупий за кв. М
= 12000 рупий
Пример 9
Пол прямоугольного двора размером 50 м на 40 м покрыт прямоугольной плиткой размеры, 1 м на 2 м.Найдите общее количество плиток, необходимых для полного покрытия пола двора.
Решение
Сначала вычислите площадь пола двора и плитки.
Площадь пола двора = (50 x 40) м 2
= 2000 м 2
Площадь плитки = (1 x 2) м 2
= 2 м 2
Чтобы найти количество плиток, необходимое для покрытия пола двора, мы делим пол двора на площадь плитки.
Количество плиток = 2000 м 2 /2 м 2
= 1000
Следовательно, для покрытия пола необходимо 1000 плиток.
Предыдущий урок | Главная страница | Следующий урокПлощадь квадрата — веб-формулы
Квадрат — это правильный многоугольник с четырьмя сторонами. У него четыре прямых угла и параллельные стороны. Чтобы вычислить площадь квадрата, умножьте основание на себя, что может быть выражено как сторона × сторона.Если квадрат имеет основание длиной 8 дюймов, его площадь будет 8 × 8 = 64 квадратных дюйма.
Площадь квадрата определяется по:
А = 2
где a = длина стороны
Периметр квадрата = 4а
Диагональ квадрата = (a) (sqrt (2)) или 1,414 (a)
Пример 1: Найдите площадь квадрата со стороной 15 м.
Решение :
Площадь квадрата = 2 = 15 2 = 225 м 2
Пример 2: Вычислите площадь квадрата, длина стороны которого составляет 35 см.
Решение :
Площадь квадрата определяется как a × a.
Площадь = 35 × 35
Площадь = 1225 см
Пример 3: Какова площадь квадратного поля, если его периметр равен 32 ярду?
Решение :
Периметр квадратного поля = 32 ярда, а поскольку периметр квадрата равен P = 4s, где s — длина стороны.Мы можем легко определить длину, выделив s из приведенной выше формулы:
с = P / 4 = 32/4 = 8 ярдов
Площадь квадратного поля = s × s
Подставляем значение s, получаем:
Площадь = 8 × 8 = 64 ярда 2
Следовательно, площадь квадратного поля составляет 64 ярда 2 .
Пример 4: Сторона квадратного парка составляет 200 м.Сколько будет стоить его озеленение при цене 0,5 доллара за кв. М?
Решение :
Что нам нужно сделать, так это найти площадь парка, а затем умножить площадь на стоимость метра 2 .
Площадь квадратного парка = сторона × сторона
A = s²
Заменить значения и упростить.
А = 200 × 200
A = 40 000 м 2
Площадь озеленения = площадь парка = 40 000 кв. М.
Стоимость посадки травы = площадь посадки травы × ставка за квадратный метр.
Подставим значения получим:
Стоимость = 40 000 x 0,5 = 20 000 долларов США.
Следовательно, стоимость посадки травы составляет 20 000 долларов США.
Пример 5: Квадратный газон окружен дорожкой шириной 2 м. Если площадь дорожки 160 кв.м, найдите площадь газона.
Решение :
Дано: Квадратный газон окружен дорожкой шириной 2 м; площадь дорожки 160 кв.м.
Найти: Площадь газона.
(Подсказка: лужайка окружена дорожкой, т. Е. Дорожка находится на внешнем крае газона. Чтобы найти площадь лужайки, вычтите площадь дорожек из общей площади)
Пусть сторона лужайки будет y, тогда у нас будет:
Внешняя сторона, включая путь = сторона лужайки + ширина дорожки с обеих сторон.
= у + (2 + 2)
= y + 4
Общая площадь, включая путь = (y + 4) × (y + 4).
= y² + 8y + 16 (i).
И площадь газона = (сторона) ² = y × y = y² (ii).
Поскольку задана площадь пути (160 м 2 ), имеем:
Площадь дорожки = Общая площадь, включая дорожку — площадь лужайки.
А = (i) — (ii).
Подставим полученные значения в следующее уравнение, и, выделив y, мы можем определить длину стороны газона:
160 = (y² + 8y + 16) — y²
160 = y² + 8y + 16 — y²
160 = y² — y² + 8y + 16
160 = 8лет + 16
160–16 = 8 лет
144 = 8лет
18 = у
Сторона газона = 18 м
Площадь газона = сторона × сторона
А = с²
А = 18 × 18
A = 324 м 2
Отсюда площадь газона = 324 м 2 .
Онлайн-калькулятор площади
Формулы площади
( пи = = 3,141592 …)
Площадь Формулы
Примечание: «ab» означает «а» умножить на «б». «a
2 » означает «квадрат», что то же самое, что «а» умножить на «а».Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений.Примеры
квадрат = a 2
прямоугольник = ab
параллелограмм = bh
трапеция = h / 2 (b 1 + b 2 )
круг = pi r 2
эллипс = pi r 1 r 2
| треугольник = | , равная половине длины основания, умноженной на высоту треугольник |
| равносторонний треугольник = |
треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C
треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)
правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = длина от центра до угла
Шт.
Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол.
Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.
Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам. 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в формате 2 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.
Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?
НЕ ПРАВИЛЬНО …. 4 раза 6 = 24
ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута.(или 2 кв. фута, или 2 фута 2 ).
Обнаружение формул площади — элементарная математика
Формулы площади
Студенты, которые неформально понимают, что область — это «количество двумерного« материала », содержащегося внутри области, могут изобрести для себя большинство формул, которые их часто просят просто запомнить. Каждая формула, которую они изобретают заново, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. Также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников.Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Прямоугольник, который в два раза больше высоты, будет иметь удвоенную площадь, поэтому площадь составляет 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же он имеет 3 ряда по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадратов, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду — это длина прямоугольника. Количество строк — это высота прямоугольника.Таким образом, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как, ну, с какой бы стороны вы его ни выбрали.
Это работает для подсчета чисел. Это работает даже для дробей. Показанный здесь синий прямоугольник измеряет половину единицы длины на пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половин площади и одну четверть единицы площади, или всего две и три четверти единицы площади.(Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить все числа , мы определяем площадь прямоугольника как основание × высота (где «основание» и «высота» означают длины , этих сторон, , измеренные в те же единицы ).
Площадь параллелограммов
Идея
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части в прямоугольник.Поскольку параллелограмм и прямоугольник состоят из одинаковых частей, они обязательно имеют одинаковую площадь. (См. Определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что у них и точно такая же базовая длина (синий) и точно такая же высота (зеленый). Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота .(Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась. Фактически, перпендикулярный разрез можно делать в любом месте по основанию.
Укрепление отверстий
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причина того, что он должен быть таким, какой он есть.Но мы не сомневались, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем, что получит , и результат определенно будет таким. Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результат не всегда является идеальным прямоугольником, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма.В старшей школе ученики смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти вскрытия работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы можем выбрать любую сторону в качестве базы; «Высота» определяется как измеряемая перпендикулярно стороне, которую мы выбираем в качестве основания. Если мы возьмем за основу короткую сторону (синюю), то рассечение, показанное выше, не будет таким убедительным.Резка на такой высоте и перестановка деталей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Оказывается, любой параллелограмм , независимо от его длины и тонкости, можно разрезать таким образом, чтобы части — возможно, многие из них — могли быть преобразованы в прямоугольник. Но нужно потрудиться, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Немного другая идея рассечения в этом случае значительно упрощает жизнь. (Самостоятельно вы можете показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, которые находятся внутри параллелограмма , а не , являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников по направлению к другому, пока они не встретятся, образуя прямоугольник. Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше), а желтая область не изменилась (части просто перемещались), разница между ними — фиолетовыми областями — должна быть такой же.Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше работы, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят , как будто они соединяются вместе, образуя прямоугольник, на самом деле точно подходят, а не просто почти .
Почему так важно быть осторожным?
При построении других формул площади (см. Ниже) мы захотим, чтобы использовал , как найти площадь параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило.Мы можем быть уверены, что перестановка частей не изменит площадь: то есть, в конце концов, как мы определяем область . Но мы также должны быть уверены, что детали подходят друг к другу, как мы утверждаем, что они делают, или мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило base × height не зависит от удачного выбора базы.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8-го класса, чтобы убедительно доказать, что эти вскрытия работают.Но интуитивного понимания достаточно для объяснения и обоснования формул и хорошей основы для дальнейшего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, помогает нам найти площадь треугольника.
Рассечение треугольника
Мы можем разрезать треугольник на две части — одну из них треугольник, а другую — трапецию, разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с этим срезом, две части сложатся вместе, образуя параллелограмм с , такое же основание , но на половину высоты .
Итак, основание × на полувысоте дает площадь треугольника. Аналогичный разрез показывает полубаз × высота . Любой из них сокращается до bh .
Удвоение треугольника и уменьшение полученной площади вдвое
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием, и такой же высотой , что и треугольник.
Площадь параллелограмма составляет основание × высота , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет из основания × высоты , как мы видели с методом рассечения.
(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции и уменьшение полученной площади вдвое
Как и в случае с треугольником, две копии трапеции можно соединить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание представляет собой сумму двух оснований трапеции.Таким образом, площадь параллелограмма равна высотой × ( base1 + base2 ). Но эта площадь составляет две трапеции, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Рассечение трапеции
Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, разрезающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого является суммой двух оснований трапеции, но высота которого равна половине высоты трапеции.
В случае трапеции основания не могут быть выбраны произвольно. Две параллельные стороны являются основаниями, а высота, как всегда, представляет собой перпендикулярное расстояние от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (полувысоте трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна полувысоте × ( основание1 + основание2 ). Поскольку параллелограмм сделан из того же материала, что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции составляет × высота × ( base1 + base2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части так, чтобы они образовали параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (а), чтобы получились два равных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
- Другой аналогичный способ — разрезать ромб на четыре равных треугольника и переставить их в прямоугольник с более короткой диагональю в качестве основания и половиной длинной диагонали в качестве высоты.
- После разрезания ромба на два равных треугольника мы можем вычислить площадь одного из треугольников, которая равна * основанию (a) * высоте (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь кайта
Площадь воздушного змея может быть похожа на площадь ромба. Если разрезать более длинную диагональ, получатся два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с более длинной диагональю (b) в качестве основания и половиной более короткой диагонали (a) в качестве высоты. Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Ну что вы знаете. По сути, вам нужно только знать формулу для площади параллелограмма, а затем вывести формулу для других.
.

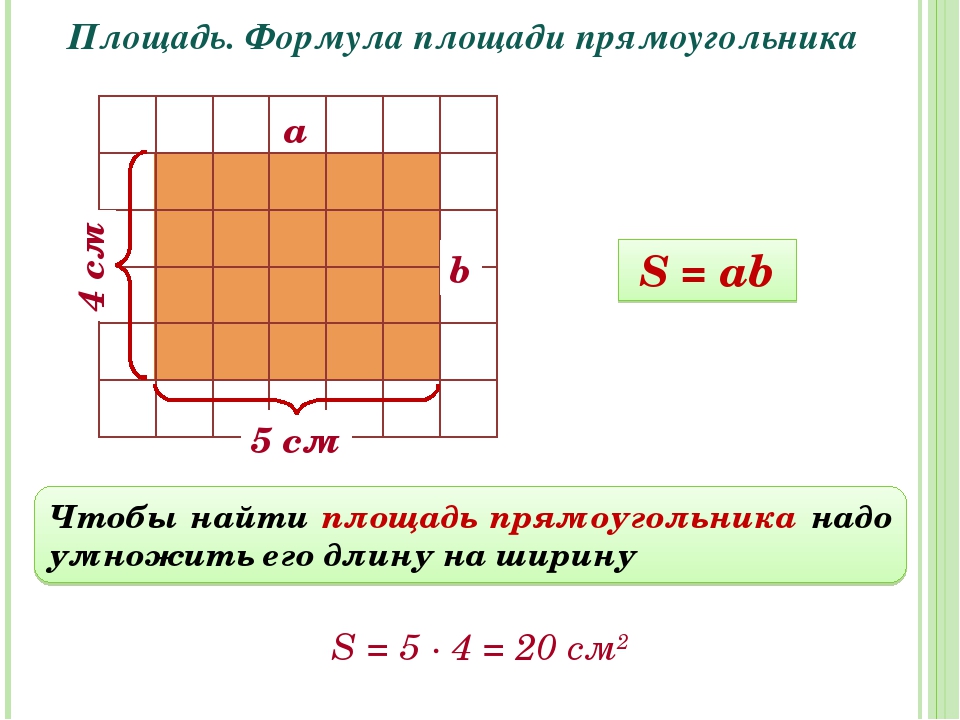
 А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.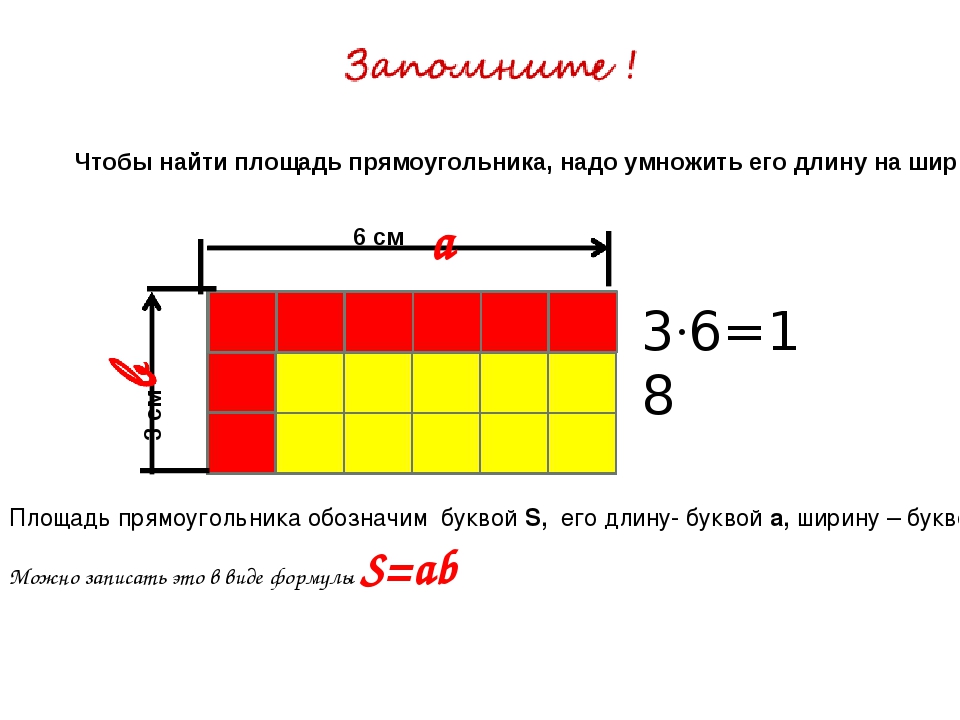 Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так: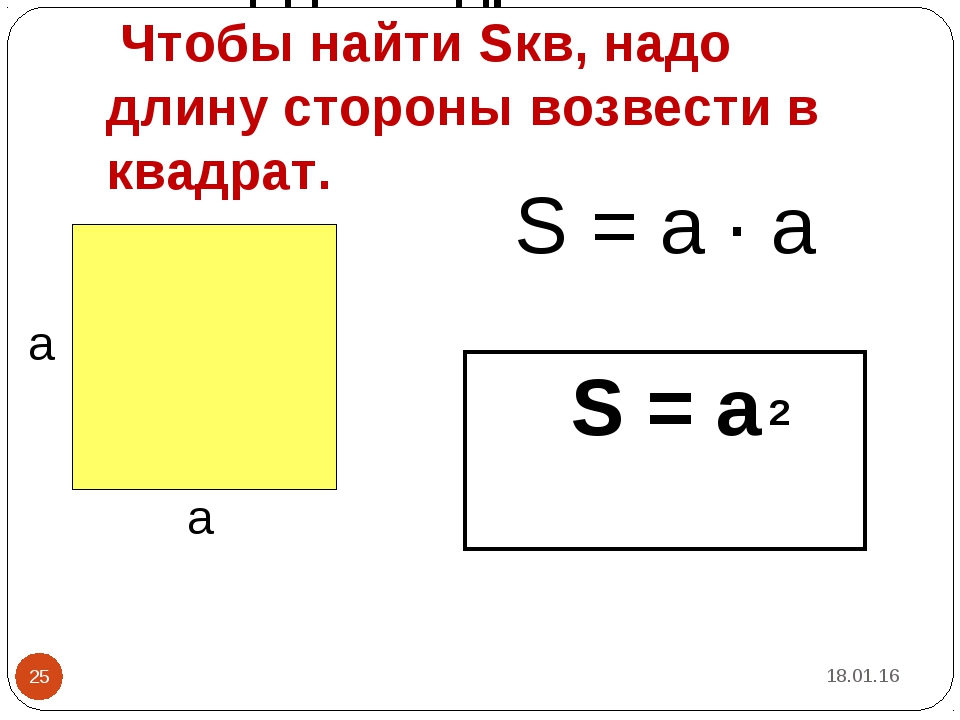

 В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.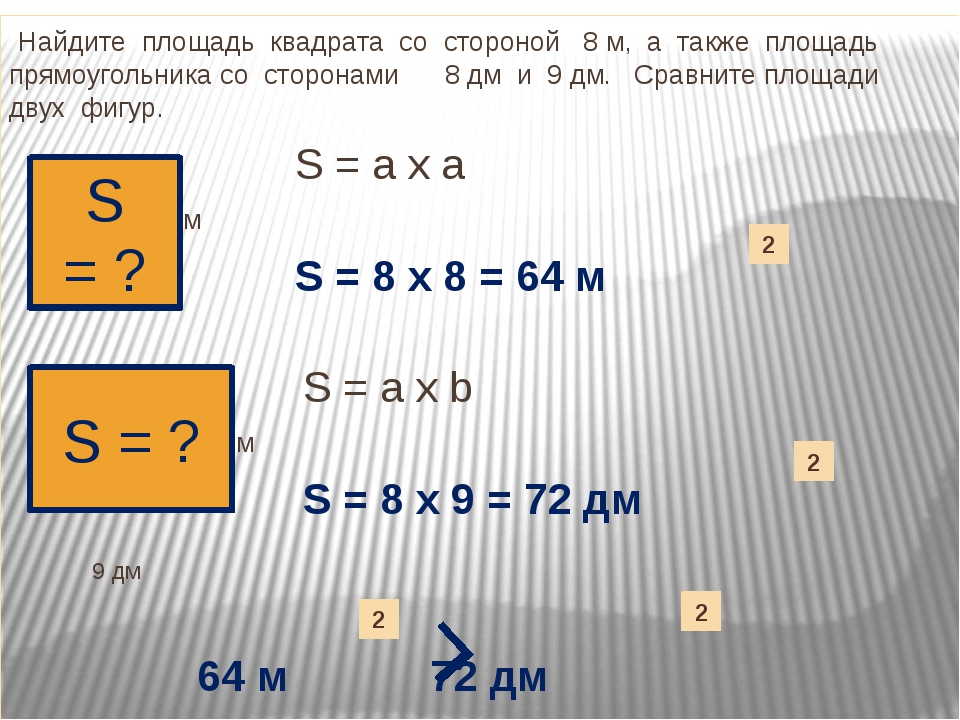 Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так: